The Fractal Stripe: One Method for Controlling the Striping of Painted Roving

A painted roving is a delicious proposition—lovely fiber, sensuous color, the promise of a unique and delightful yarn. We usually want to jump right in and start spinning, but we often end up with surprising results. Sometimes they are good surprises when the roving turns into a yarn more beautiful than the one we imagined, and sometimes the results are disappointing when the clarity of the roving’s colors turn to mud. Often, spinners are mystified about predicting what the colors of their fiber will do when spun. If you take the time to analyze how to prepare and spin the fiber, you can control the resulting yarn.

There are three major factors to consider when predicting the outcome of your striped yarn: scale, direction, and color. I will first analyze the role of scale and direction relative to the fractal stripe (a fractal is a mathematical definition of a pattern in which the element is repeated on a smaller and smaller scale into infinity). Color theory is a subject too large for this article (see Deb Menz’s book Color Works for a thorough treatment of the topic); however, we will explore a few principles very briefly.

The first step in working with painted roving is to analyze it. Is it space-dyed or random-dyed? If it is randomly dyed, then you will get random results. You can influence your results a little, but for the most part, you just go with the flow and get wonderful random striping and blending. If, on the other hand, your painted fiber is space-dyed, then you can manipulate it to get the type of effect you want.

Scale

The first aspect to notice about scale is in the dye job itself. Here are some questions to ask about your roving that can affect the outcome.

• Does your fiber have long or short stretches of color?
• Are the relative scales of the colors even, or does one color have a longer stretch than the others?
• Is the roving dyed evenly, and does each occurrence of color roughly match the size and intensity of other occurrences of the same color?

The answer to the first question, concerning long or short stretches of color, determines the size of your stripes. It sounds obvious, but it is worth stating that a roving with short stretches of color will change colors more quickly than one with long stretches of color. The answer to the second question determines the overall tone of your finished yarn. In a roving where one color has a longer stretch than the others, the color with the long stretch will dominate your finished yarn. To verify this, take your roving and twist it together like a skein. Slightly squint your eyes to look at it and notice which color dominates. The third question concerns the regularity of your stripes. If your roving is dyed fairly evenly and you spin it in a controlled manner, you can achieve even striping of your yarn.

You can affect the scale of the stripes in your yarn by your preparation for spinning it. If you want the striping to appear more frequently with smaller stripes, strip the roving into smaller widths. If you want your striping to appear less frequently and have large stripes, use the roving in its original width.

If you like to attenuate your fiber by gently pulling from one end to loosen the fibers and make a thinner roving, be aware that this will not affect the ultimate size of your stripes. Although it may look thinner in your hand as you spin, you still have the same amount of each color, as long as you spin to the same grist as with a thicker strip of roving.

Direction

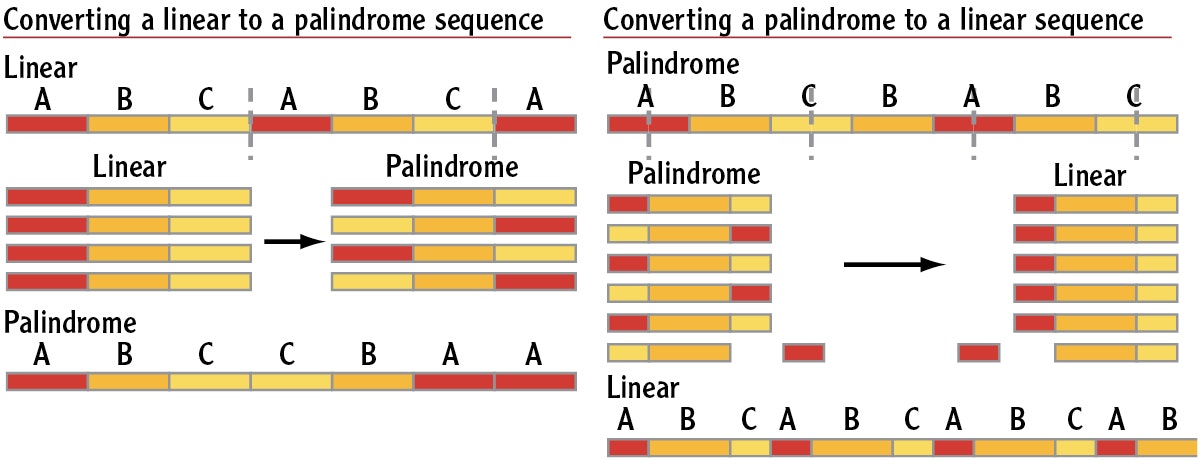
Many times we don’t notice that a space-dyed roving has a particular sequence or direction to the colors. Typically a roving will have either a linear or a palindrome sequence.[PAYWALL]

A linear sequence is one in which the elements repeat by starting again at the beginning. I call this the ABCABC method, or, if you like to think in colors, it might be red, orange, yellow, red, orange, yellow. If you spin a roving with this type of sequence, you get a linear feeling of movement in your stripes. They seem to zip along in one direction or the other.

A linear sequence is one in which the elements repeat by starting again at the beginning.

A palindrome sequence is one in which the elements repeat by mirror inversion. I call this the ABCBA sequence, or red, orange, yellow, orange, red. If you spin a roving with this sequence, you get a feeling of undulating movement in your stripes—they crest hills and dip into valleys.

A palindrome sequence is one in which the elements repeat by mirror inversion.

If you have one of these sequences and want the other, you can change it to the other! The key is in knowing where to break the fiber. If, for example, you have a linear sequence and you want it to be a palindrome, just break the sequence right at the division between two colors. If your fiber’s sequence is red, orange, yellow, red, orange, yellow, you may choose to break it between the yellow and the red. Break the entire roving between every yellow and red in the sequence and then lay out all the pieces in the same direction. You will have several sections of red, orange, yellow. Take half of the pieces and turn them in the opposite direction, so that half of your sequences are now red, orange, yellow and the other half are yellow, orange, red. When you spin, first pick up a red, orange, yellow, next pick up a yellow, orange, red, then a red, orange, yellow, and so on. Voilà! You have changed a red, orange, yellow, red, orange, yellow into a red, orange, yellow, yellow, orange, red.

Similarly, you can also change a palindrome sequence into a linear sequence. The key here is to divide right in the middle of both of the center colors. (A center color is a color flanked on either side by the same color.) If your sequence is red, orange, yellow, yellow, orange, red, you have two center colors, yellow and red. Divide in the center of both the yellow and the red, then turn half of the pieces around so that the sequences of all the pieces are now going in the same direction and spin. Note that when you’re changing from one type of sequence to the other, you are also changing the relative scale of your colors. In the first case, when you are going from linear to palindrome, you end up with back to back (double) yellows and reds, which makes your orange small in relation to the yellow and red. In the second case, when you are going from palindrome to linear, you end up with half reds and half yellows making your orange relatively large. You can use this method to introduce more movement into your color sequence since differential scales appear to us to have more movement than a static scale.

Color

Color is a large topic, but there are a few rules that we can discuss relative to the striping of space-dyed fiber.

• More colors give more visually complex striping patterns. A roving with only two colors produces very clear striping patterns.
• Analogous colors have more subtle striping effects than complements or triads.
• Colors of the same value have more subtle striping effects than a combination of different values.
• Bright hues tend to dominate when in equal proportion to tonal hues; light values tend to dominate when in equal proportion to dark values.

The fractal stripe

One of my favorite ways to treat a spacedyed roving is to spin it into a fractal stripe. As I mentioned earlier, a fractal is a mathematical definition of a pattern in which the element is repeated on a smaller and smaller scale into infinity. I loosely call this method a fractal stripe since, of course, no one wants to spin into infinity!

The fractal stripe takes advantage of differential scales to control the effective striping in your finished piece. To achieve the simplest fractal stripe, divide your roving in half. Spin one-half of it as it came. Spin the other half by stripping it lengthwise into smaller widths. Keep the sequence of each strip in the same order as the first half and spin them sequentially. Now ply each of these halves into a two-ply yarn. What happens in your finished yarn is that you have one ply’s stripe repeating over a large scale and giving a background to your second ply, which is striping much more frequently and in thinner stripes. At the same time, each set of stripes follows the same sequence. The greater the difference in scale, the more distinct your striping will appear because your eye can more clearly perceive the patterning.

Figure 1 shows the efects of analogous and split complement color schemes. All figure photos by Janel Laidman

Figure 2 shows a roving that was spun in this manner. You can clearly see the large yellow-green, blue, and lavender stripes repeating in sequence. They look like large swaths of different colors in the swatch. Within these large stripes the same sequence repeats on a smaller scale. It’s fun to look at how a different background causes stripes of the same color to appear different. You can achieve different effects in the fractal stripe by playing with different scales. In figures 1 and 2, I kept one-half of the fiber the full width of the roving, and I stripped the second half into twelve finger-width strips. In figure 3, I kept one-half of the fiber the full width of the roving and stripped the second half into fourths. I then spun and plied them into a two-ply yarn. The greater scale differential in figure 1 results in more defined regions of color, whereas the smaller scale differential in figure 3 results in a more blended look because the larger “background” stripe is much less dominant in relation to the “foreground” stripe. Contributing to this effect is the fact that the colors in figure 1 are brighter and more dominant, whereas the colors in figure 3 are darker in value and recede into each other.

In figure 2, you can clearly see the large yellow-green, blue, and lavender stripes repeating in sequence.

In figure 1, you can see the effects of analogous and split complement color schemes. The roving used in figure 1 is brick red, orange-brown, and turquoise. This is known as a split complement because of the relationship of these colors on the color wheel. Analogous colors are those that are next to each other on the color wheel. If we throw out the turquoise, the brick red and orange-brown are an analogous color set (for more discussion of these relationships on the color wheel, see Deb Menz’s book Color Works). In section one of figure 2, the background colors are analogous and the effect is subtle. The small stripe of turquoise in the foreground ply (still a split complement) really pops out. On the other hand, if you look at the overall sample including the turquoise, you can see that including the complement in the background gives a much bolder effect.

You can also affect the fractal stripe by playing with the scale of the plies. In figure 4, I divided my roving into thirds. I spun two-thirds of the roving as it was, without stripping, and spun that fiber into a thick singles. I stripped the remaining third and spun it in a thinner singles (half the size of the first one). I then plied them together. The result is that the large stripe dominates the overall finished piece, while the thin stripes fade into the background like white noise. The size differential in the plies means that the striping of one ply will dominate the other. You could also choose to do this in the opposite manner, by spinning the smaller striping single thick and the larger striping singles thin. This is an interesting alternative to Navajo plying when you want to preserve the sequence of colors without muddyin them. There is more color interference than in straight Navajo three-ply, but you can control that by choosing a ply size differential to either play up the interference or minimize it. The advantages to this method are that you don’t have to do tricky chaining maneuvers while plying and you can get a nice, smooth two-ply yarn. Remember when using the ply differential method that a thicker ply will eat up the fiber faster than a thinner ply, so plan accordingly when you split the fiber. By playing with the fractal stripe you can achieve a wide variety of striping effects from bold to subtle. If your colors are analogous and of similar value and your sequence is a palindrome, your outcome might be a subtle undulation from one dominating hue to another. If your colors are bright, clear complements with a linear sequence, your outcome might be a vibrant (nearly vibrating!) dazzle of the senses. I hope that you will take this method and try some combinations of your own.

Resources

• Menz, Deb. Color Works. Loveland, Colorado: Interweave Press, 2004.
• Itten, Johannes. The Elements of Color: A Treatise on the Color System of Johannes Itten Based on His Book the Art of Color. New York: Van Nostrand Reinhold, 1971.

This article originally appeared in the Summer 2007 issue of Spin Off. Originally published January 20, 2020; updated March 5, 2025.

Also, remember that if you are an active subscriber to Spin Off magazine, you have unlimited access to previous issues, including Summer 2007, in the Spin Off Library.

Janel Laidman is the author of The Painted Skein (2007).